The Kolmogorov-Smirnov test, often referred to as the K-S test, is a non-parametric statistical test used to assess whether a dataset follows a particular probability distribution or to compare the distributions of two datasets. Andrey Kolmogorov and Nikolai Smirnov developed it, hence the name.
There are two main variations of the Kolmogorov-Smirnov test:
- One-Sample Kolmogorov-Smirnov Test: This variation is used to determine whether a single sample of data follows a specified probability distribution. The most common use is to test whether a sample of data follows a known theoretical distribution, like the normal distribution. The test statistic is based on the maximum absolute difference between the empirical distribution function (EDF) of the sample and the cumulative distribution function (CDF) of the theoretical distribution.
- Two-Sample Kolmogorov-Smirnov Test: This version is used to compare two independent samples to determine if they come from the same distribution or if they are significantly different. It tests whether the two datasets have similar distributions. In this case, the test statistic is based on the maximum vertical distance between the two empirical distribution functions.
One-Sample Kolmogorov-Smirnov Test
The one-sample Kolmogorov-Smirnov test is used to determine whether a sample follows a specified distribution, such as a normal distribution. To perform this test in R, follow these steps:
Step 1: Load Your Data
Load your dataset into R using functions like read.csv() or read.table() or create a vector with your data.
# Load your data (example using a vector) data <- c(2.5, 3.1, 2.9, 2.7, 3.2, 3.4, 3.0, 2.8, 2.6, 3.5)
Step 2: Perform the Test
Use the ks.test() function to perform the one-sample Kolmogorov-Smirnov test. In this example, we will test whether the data follows a normal distribution.
# Perform the one-sample Kolmogorov-Smirnov test ks_result <- ks.test(data, "pnorm", mean = mean(data), sd = sd(data))
Here, we specify "pnorm" as the reference distribution, indicating a normal distribution. You should replace this with the appropriate distribution for your data.
Step 3: Interpret the Results
Now, let’s interpret the results:
# Print the test result
print(ks_result)
# Extract p-value from the result
p_value <- ks_result$p.value
# Decide on significance level (e.g., 0.05)
alpha <- 0.05
# Check the p-value against the significance level
if (p_value < alpha) {
cat("The data does not follow a normal distribution (reject the null hypothesis).")
} else {
cat("The data follows a normal distribution (fail to reject the null hypothesis).")
}
This code will output whether your data follows the specified distribution.
> print(ks_result)
Exact one-sample Kolmogorov-Smirnov test
data: data
D = 0.10136, p-value = 0.9995
alternative hypothesis: two-sided
> # Check the p-value against the significance level
> if (p_value < alpha) {
+ cat("The data does not follow a normal distribution (reject the null hypothesis).")
+ } else {
+ cat("The data follows a normal distribution (fail to reject the null hypothesis).")
+ }
The data follows a normal distribution (fail to reject the null hypothesis).
Two-Sample Kolmogorov-Smirnov Test
The two-sample Kolmogorov-Smirnov test is used to compare the distributions of two samples. It’s often used to determine if two datasets come from the same population or if they are significantly different. Here’s how to perform this test in R:
Step 1: Load Your Data
Load or create two datasets that you want to compare.
# Load or create two datasets (example using vectors) data1 <- c(23, 27, 29, 30, 35, 38, 40, 42, 44, 45) data2 <- c(19, 25, 27, 31, 36, 38, 41, 43, 46, 48)
Step 2: Perform the Test
Use the ks.test() function for the two-sample Kolmogorov-Smirnov test:
# Perform the two-sample Kolmogorov-Smirnov test ks_result <- ks.test(data1, data2)
Step 3: Interpret the Results
Interpret the results as follows:
# Print the test result
print(ks_result)
# Extract p-value from the result
p_value <- ks_result$p.value
# Decide on significance level (e.g., 0.05)
alpha <- 0.05
# Check the p-value against the significance level
if (p_value < alpha) {
cat("The two datasets have significantly different distributions (reject the null hypothesis).")
} else {
cat("The two datasets have similar distributions (fail to reject the null hypothesis).")
}
This code will output whether the two datasets have significantly different distributions.
> print(ks_result)
Exact two-sample Kolmogorov-Smirnov test
data: data1 and data2
D = 0.2, p-value = 0.9917
alternative hypothesis: two-sided
> # Check the p-value against the significance level
> if (p_value < alpha) {
+ cat("The two datasets have significantly different distributions (reject the null hypothesis).")
+ } else {
+ cat("The two datasets have similar distributions (fail to reject the null hypothesis).")
+ }
The two datasets have similar distributions (fail to reject the null hypothesis).
In both one-sample and two-sample Kolmogorov-Smirnov tests, the null hypothesis is that the data follows the specified distribution or the two datasets have the same distribution. A small p-value indicates a rejection of the null hypothesis, suggesting a significant difference between the data or datasets. Conversely, a large p-value suggests that the data or datasets do not significantly differ from the specified distribution or each other.
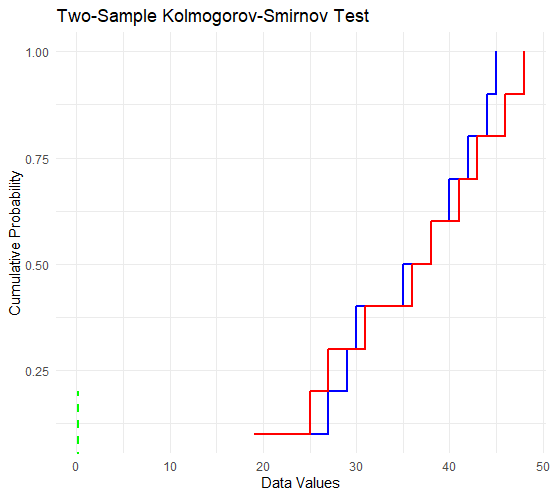
Two-sample Kolmogorov-Smirnov test Visualization
To visualize the results of a two-sample Kolmogorov-Smirnov test, you can create an empirical distribution plot for both datasets and highlight the maximum vertical distance (D-statistic) between the two cumulative distribution functions.
# Load required packages library(ggplot2) # Create or load two datasets data1 <- c(23, 27, 29, 30, 35, 38, 40, 42, 44, 45) data2 <- c(19, 25, 27, 31, 36, 38, 41, 43, 46, 48) # Perform the two-sample Kolmogorov-Smirnov test ks_result <- ks.test(data1, data2) # Create a cumulative distribution function (CDF) plot for both datasets ecdf_data1 <- ecdf(data1) ecdf_data2 <- ecdf(data2) # Plot the CDFs ggplot() + geom_step(aes(x = data1, y = ecdf_data1(data1)), color = "blue", linetype = "solid", size = 1) + geom_step(aes(x = data2, y = ecdf_data2(data2)), color = "red", linetype = "solid", size = 1) + geom_segment(aes(xend = ks_result$statistic, yend = ks_result$statistic), x = ks_result$statistic, y = 0, linetype = "dashed", color = "green", size = 1) + labs(x = "Data Values", y = "Cumulative Probability", title = "Two-Sample Kolmogorov-Smirnov Test") + theme_minimal()